Exercises (CT Chapter 7)

I don’t really have a lot of exercises for the chapter on recursion. I had planned to combine recursion with divide-and-conquer, but now the two topics are split over two weeks. Instead, I will have a project for the students to do while they learn about recursion; then it doesn’t matter so much that there are not that many exercises.

Anyway, exercises below and answers below that.

Exercises

Fibonacci

Exercise: Implement a recursive function that computes the n’th Fibonacci number.

Exercise: Draw the call stack for computing the fourth Fibonacci number using the implementation you did in the previous exercise.

List exercises

Exercise: To compute the sum of the elements in a list, we can obviously do this iteratively:

result = 0
for e in x:
  result += e

Implement a recursive function that computes the sum of the elements of a list.

Exercise: We can find the smallest element in a non-empty list, x, like this:

smallest = x[0]
for e in x:
	smallest = min(smallest, e)

Write a recursive function for finding the smallest element in a list. To avoid copying the list using slices, you will want to have the function take an index parameter as an argument.

Exercise: Modify your function, so it returns None if the list is empty. The easiest way to do this is probably to include the “smallest element seen so far” as a parameter to the function, with a default value of None. To compute the smallest value and still handle None you can use this function:

def my_min(x, y):
	return y if x is None else min(x, y)

Exercise: Write a recursive function that reverses a list.

Exercise: Recall the exercise where you had to translate a base-10 number into some other base b (where we restricted the base to be less than 16). We can get the last digit of a number i, in base b using this function:

def get_last_digit(i, b):
    return digits[i % b]

where we defined the digits list as

digits = {}

for i in range(0,10):
    digits[i] = str(i)

digits[10] = 'A'
digits[11] = 'B'
digits[12] = 'C'
digits[13] = 'D'
digits[14] = 'E'
digits[15] = 'F'

We can then reduce the problem to the second-to-last digit by dividing i by b. Implement this idea using a recursive function.

Tail-Recursion

Exercise: Rewrite your recursive function for computing the sum of a list of numbers such that it becomes tail-recursive.

Exercise: Rewrite your recursive function for finding the smallest element in a list to a version that is tail-recursive.

Exercise: Do the tail-recursion transformation for your tail-recursive summation function.

Exercise: Do the tail-recursion transformation for your tail-recursive “find minimum” function.

Exercise: Consider our recursive implementation of binary search:

def bsearch(x, e, low = 0, high = len(x)):
	if low >= high:
		return False
	mid = (low + high) // 2
	if x[mid] == e:
		return True
	elif x[mid] < e:
		return bsearch(x, e, mid + 1, high)
	else:
		return bsearch(x, e, low, mid)

This function is tail-recursive, so use the transformation to replace it with a loop. Compare it to the iterative solution we considered before this chapter.

Answers

Fibonacci

Exercise: Implement a recursive function that computes the n’th Fibonacci number.

def Fib(n):
    if n <= 2: return 1
    else: return Fib(n - 1) + Fib(n - 2)

Exercise: Draw the call stack for computing the fourth Fibonacci number using the implementation you did in the previous exercise.

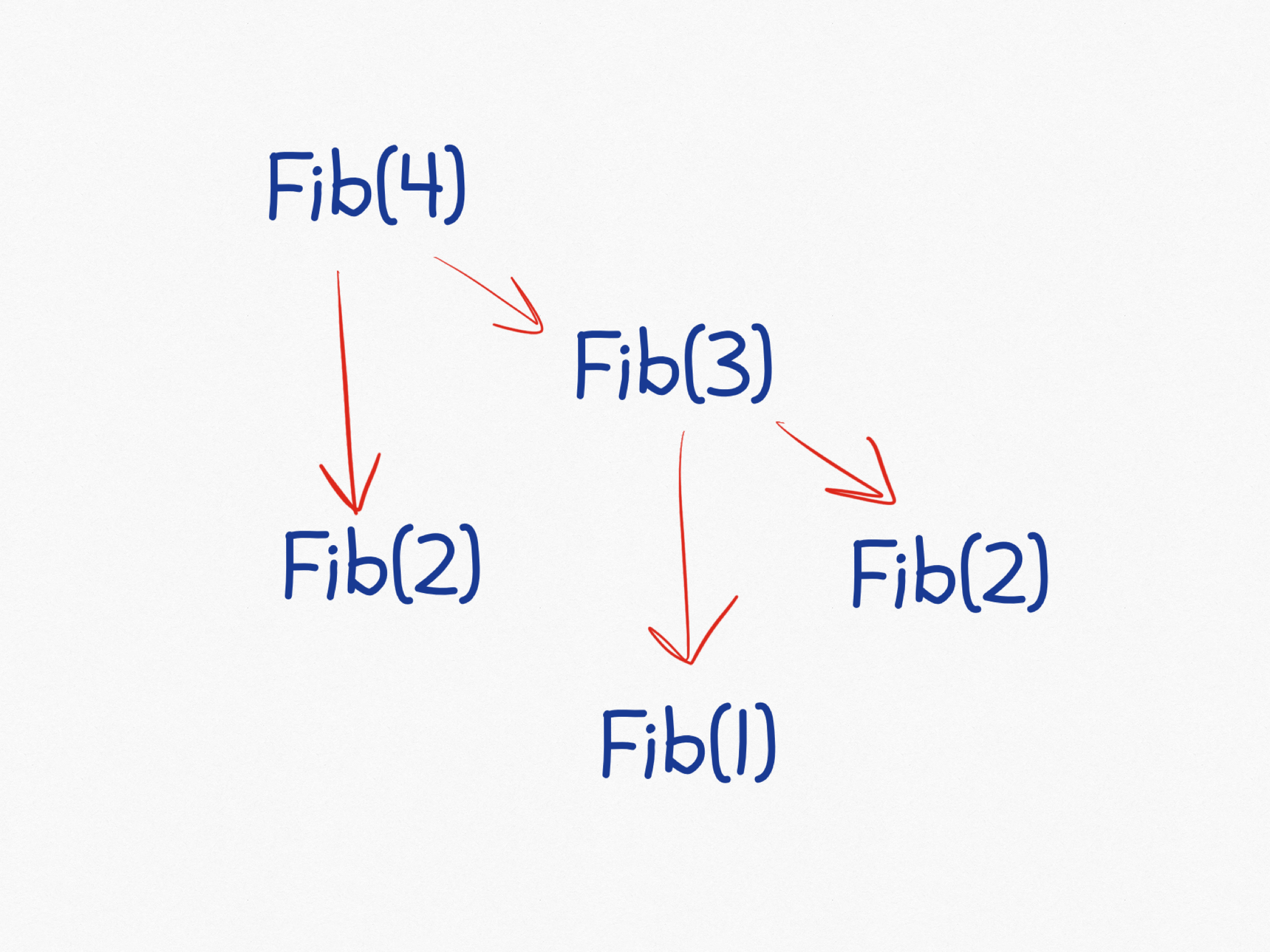
List exercises

Exercise: To compute the sum of the elements in a list, we can obviously do this iteratively:

result = 0
for e in x:
  result += e

Implement a recursive function that computes the sum of the elements of a list.

def recsum(x):
    if x == []: return 0
    else: return x[0] + recsum(x[1:])

Exercise: We can find the smallest element in a non-empty list, x, like this:

smallest = x[0]
for e in x:
	smallest = min(smallest, e)

Write a recursive function for finding the smallest element in a list. To avoid copying the list using slices, you will want to have the function take an index parameter as an argument.

def min_rec(x, i = 0, acc = None):
    if i == len(x): return acc
    acc = x[i] if acc is None else min(acc, x[i])
    return min_rec(x, i + 1, acc)

Exercise: Modify your function, so it returns None if the list is empty. The easiest way to do this is probably to include the “smallest element seen so far” as a parameter to the function, with a default value of None. To compute the smallest value and still handle None you can use this function:

def my_min(x, y):
	return y if x is None else min(x, y)

My solution from above already works this way.

Exercise: Write a recursive function that reverses a list.

def reverse_rec(x, acc = []):
    if x == []: return acc
    return reverse_rec(x[1:], [x[0]] + acc)

This implementation is very inefficient due to how Python lists are implemented. It would be very efficient if we used linked lists. With array-like vectors, we wouldn’t usually need recursion—it is easier to solve that reversal problem iteratively.

Exercise: Recall the exercise where you had to translate a base-10 number into some other base b (where we restricted the base to be less than 16). We can get the last digit of a number i, in base b using this function:

def get_last_digit(i, b):
    return digits[i % b]

where we defined the digits list as

digits = {}

for i in range(0,10):
    digits[i] = str(i)

digits[10] = 'A'
digits[11] = 'B'
digits[12] = 'C'
digits[13] = 'D'
digits[14] = 'E'
digits[15] = 'F'

We can then reduce the problem to the second-to-last digit by dividing i by b. Implement this idea using a recursive function.

def to_base(n, b, rev_digits = None):
    # get an empty list if argument is None
    rev_digits = rev_digits or []

    if n == 0:
        if rev_digits == []: return "0"
        return "".join(reversed(rev_digits))
    else:
        rev_digits.append(digits[n % b])
        return to_base(n // b, b, rev_digits)

Tail-Recursion

Exercise: Rewrite your recursive function for computing the sum of a list of numbers such that it becomes tail-recursive.

def recsum_tr(x, acc = 0):
    if x == []: return acc
    else: return recsum_tr(x[1:], acc + x[0])

Exercise: Rewrite your recursive function for finding the smallest element in a list to a version that is tail-recursive.

def min_rec(x, i = 0, acc = None):
    if i == len(x): return acc
    acc = x[i] if acc is None else min(acc, x[i])
    return min_rec(x, i + 1, acc)

Exercise: Do the tail-recursion transformation for your tail-recursive summation function.

def recsum_tr(x, acc = 0):
		while True:
		    if x == []: return acc
		    x, acc = x[1:], acc + x[0]

Exercise: Do the tail-recursion transformation for your tail-recursive “find minimum” function.

def min_rec(x, i = 0, acc = None):
		while True:
		    if i == len(x): return acc
		    acc = x[i] if acc is None else min(acc, x[i])
		    i += 1

Exercise: Consider our recursive implementation of binary search:

def bsearch(x, e, low = 0, high = len(x)):
	if low >= high:
		return False
	mid = (low + high) // 2
	if x[mid] == e:
		return True
	elif x[mid] < e:
		return bsearch(x, e, mid + 1, high)
	else:
		return bsearch(x, e, low, mid)

This function is tail-recursive, so use the transformation to replace it with a loop. Compare it to the iterative solution we considered before this chapter.

The direct translation is this:

def bsearch(x, e, low = 0, high = len(x)):
    while True:
	    if low >= high:
		    return False
	    mid = (low + high) // 2
	    if x[mid] == e:
		    return True
	    elif x[mid] < e:
		    return bsearch(x, e, mid + 1, high)
	    else:
		    return bsearch(x, e, low, mid)

If we just change the loop condition we get the usual function:

def bsearch(x, e, low = 0, high = len(x)):
    while low < high:
	    mid = (low + high) // 2
	    if x[mid] == e:
		    return True
	    elif x[mid] < e:
		    return bsearch(x, e, mid + 1, high)
	    else:
		    return bsearch(x, e, low, mid)
    return False